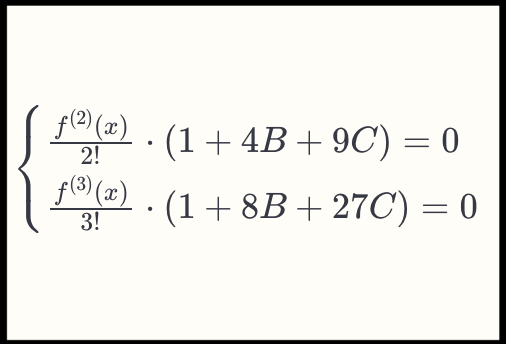はじめに
解析解(数学解)が求められない場合に、数値解析で数値解を計算しますが、計算機で扱うためには離散化が必要です。ここでは、微分方程式を解く時に必要な離散化を考えます。微分方程式を解くための離散化には、時間の離散化と、空間の離散化があります。離散化で最もよく使われるのが差分法であり、前進差分、後退差分、中央差分があります。
空間の離散化には、最も直感的な中央差分が使われることが多いように思います。もっとも、扱う系によって異なりますし、格子状に離散化しない場合、例えば粒子法による流体計算は最も狭い意味での中央差分ではありません。概念的には中央での離散化を行っているのは同じですが、その具体的な計算方法が格子を基本とする差分法とは異なります。
時間の離散化には、陽解法では前進差分、陰解法では後退差分、クランク・ニコルソン法というものでは中央差分を使うものとなっていて、一長一短があります。陽解法はシンプルに現在の状態を元に漸化式を解くイメージで次の時刻の状態を計算するもので、実装が簡単ですが、必ずしも数値的に安定で収束するわけではないため、時間ステップを大きく取れません。陰解法は現在の状態がどのようなものであれば一つ前の状態と適合するかを解くもので、連立方程式を解く必要があり、実装が複雑ですが、時間ステップを大きく取れるため、シミュレーション時間が長い時には有利です。クランク・ニコルソン法は、これも実装が複雑ですが、離散化誤差は最も小さくなります。クランク・ニコルソン法では、ステップの中央に注目して微分方程式を解きますが、離散化した時にそこには格子点が存在しないため、両脇の格子点の平均を近似として用います。
陰解法、クランク・ニコルソン法はともに数値的に安定な(情報が伝播する速さが、実際の物理現象の伝播する速さよりも早くあります必要があるという、CLF条件による制約がない)ので、時間ステップは離散化誤差が許容できる範囲で大きく取れることになります。なお、CLF条件は必要条件ですが、それ以外に安定性の解析方法にフォン・ノイマンの安定性解析があります。これは、差分法でどの精度の差分式を使うかによって異なる打ち切り誤差が、計算の過程で収束するか発散するかを解析するものです。これは解きたい微分方程式によって異なる結果を出しますが、時間ステップ幅と空間ステップ幅の関係がどうであれば打ち切り誤差が収束するかがわかります。ここでは割愛しますが、連立方程式を解くときの行列の固有値が関係します。
1次精度の差分式の導出
関数の微分値を差分法で表すには、関数のテイラー展開を元にして計算を行います。何次の項まで使うかによって精度が異なります。これによって、差分法には、(前進, 後退, 中央)差分×(N回微分)×(M次精度)というような組み合わせがあり得ることになります。
まず、前進と後退のテイラー展開から、1階微分の差分式を導出してみます。f(x)のn階微分を次のように書くことにします。
f^{(n)}(x)前進差分
数式(1): hだけ前進させます。
f(x+h)=\sum^{\infty}_{n=0}\frac{f^{(n)}(x)}{n!}h^n=f(x)+f^{(1)}(x)\cdot h+\frac{f^{(2)}(x)}{2!}h^2+\frac{f^{(3)}(x)}{3!}h^3+...数式(2): ここから、1階1次精度の前進差分を求めることができます。
f^{(1)}(x)=\frac{f(x+h)-f(x)}{h}+\mathcal{o}(h)後退差分
数式(3): hだけ後退させます。
f(x-h)=\sum^{\infty}_{n=0}\frac{f^{(n)}(x)}{n!}(-h)^n=f(x)-f^{(1)}(x)h+\frac{f^{(2)}(x)}{2!}h^2-\frac{f^{(3)}(x)}{3!}h^3+...数式(4):ここから、1階1次精度の後退差分を求めることができます。
f^{(1)}(x)=\frac{f(x-h)-f(x)}{-h}+\mathcal{o}(h)中央差分
数式(5): 前進差分と後退差分のテイラー展開の差をとると、右辺の奇数番目の項が消えます。
f(x+h)-f(x-h)=2(f^{(1)}(x) \cdot h+\frac{f^{(3)}(x)}{3!}h^3+\frac{f^{(5)}(x)}{5!}h^5+...)数式(6): ここから1階2次精度の中央差分が計算できます。
f^{(1)}(x)=\frac{f(x+h)-f(x-h)}{2h}+\mathcal{o}(h^2)高次精度の差分式の導出
ここからは、高次精度の差分式をみたいと思います。前進差分と中央差分について書いていきますが、後退差分についてはhを-hに読み換えて下さい。
2次精度の前進差分式
数式(7): 前進差分で2h先をみたときのテイラー展開
f(x+2h)=\sum^{\infty}_{n=0}\frac{f^{(n)}(x)}{n!}(2h)^n=f(x)+f^{(1)}(x)\cdot 2h+\frac{f^{(2)}(x)}{2!}(2h)^2+\frac{f^{(3)}(x)}{3!}(2h)^3+...数式(8): (1)式の4倍から(7)式を引いてf(x)の1階微分について整理するとh^2の項が消えて、2次精度の差分式ができます。
f^{(1)}(x)=\frac{-f(x+2h)+4f(x+h)-3f(x)}{2h}+\mathcal{o}(h^2)3次精度の前進差分式
数式(9): 2次精度のときと同様に、前進差分で3h先をみたときのテイラー展開
f(x+3h)=\sum^{\infty}_{n=0}\frac{f^{(n)}(x)}{n!}(3h)^n=f(x)+f^{(1)}(x)\cdot 3h+\frac{f^{(2)}(x)}{2!}(3h)^2+\frac{f^{(3)}(x)}{3!}(3h)^3+...数式(10): (h以外の)h^2とh^3の項を消すために、(1)式-(7)式*(-1/2)+(9)式*(1/9)を計算し、f(x)の1階微分について整理すると
f^{(1)}(x)=\frac{2f(x+3h)-9f(x+2h)+18f(x+h)-11f(x)}{6h}+\mathcal{o}(h^3)なお、-1/2, 1/9という数字をどうやって出すかというと、繰り返しになりますがh^2とh^3の項の係数がゼロとなるように、係数についての連立方程式を解いて求めることになります。
数式(11): 具体的には次の連立方程式を解きました。
\left\{\begin{array}{l}\frac{f^{(2)}(x)}{2!} \cdot(1+4B+9C)=0\\\frac{f^{(3)}(x)}{3!} \cdot(1+8B+27C)=0\end{array}\right.これを解くと、B=-1/2, C=1/9となります。
任意精度の前進差分式
ここまでやると、N階M次精度微分の前進差分式を一般的に決定できることがわかります。つまり、h, 2h, 3h, ...Mhまで先をみたテイラー展開を行い、h^N以外のh冪乗の項を消去できるように係数についての連立方程式を立てて解けばよいのです。このとき、M > Nでないと連立方程式が解けません。これは直感的にも、N階微分の計算にN+1個以上の点が必要ですということと一致します。
任意精度の後退差分式
最初に注意したように、hを-hに読み替えることで、同じようにN階M次精度微分の後退差分を計算できます。
任意精度の中央差分式
さて、2階微分の中央差分式も考えてみます。
数式(12): まずはhまで先をみた前進と後退のテイラー展開を行った和を考えます。和にしたのはh^2の項を消さないためです。これは、h^2の項まで捉えているので、2次精度です。
f^{(2)}(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^2} +\mathcal{o}(h^2)続いて、1階微分の4次精度の中央差分式を考えます。
数式(13): 2hまで先をみた前進と後退のテイラー展開を行った差を考えると(5)式と同様に
f(x+2h)-f(x-2h)=2(f^{(1)}(x) \cdot 2h+\frac{f^{(3)}(x)}{3!}(2h)^3+\frac{f^{(5)}(x)}{5!}(2h)^5+...)(5)式と(13)式を足し引きして、右辺h^3の項の係数がゼロになるようにしたい、と考えます。
右辺では求めたいf(x)の1階微分にhがかかっていることに注意してください。4次精度なのでh^5の項は消さないし、消そうにも式の本数が足りません。消すなら3hまで先をみたテイラー展開の式との連立が必要です。そのとき6次精度となります。
数式(14): 結局のところ、(13)式ではh^3の項の係数が(5)式の8倍なので、(5)式*8-(13)式を計算してf(x)の1階微分について整理すると
f^{(1)}(x)=\frac{f(x+2h)-8f(x+h)+8f(x-h)-f(x-2h)}{12h}+\mathcal{o}(h^4)ここでも、前進差分の時と同様に、N階の2M-1または2M次精度の中央差分式が計算できるとわかります。手順としては、前後にh, 2h, 3h, ... Mhまでみたテイラー展開を行い、Nが奇数なら前進と後退のテイラー展開の差を、Nが偶数なら和を取るところから始めます。そして、求めたいh^Nの項以外の係数を消去できるように、係数についての連立方程式を立てて解けばよいことになります。
さいごに
さて、前進差分、後退差分、中央差分の違いは何かというと、文字通りに読めば、どこを差分の中心とするかということです。問題によって使い分けるのが良く、必要に応じてこれらの差分式を混合することで、差分の中心を任意の場所に置くことができます。