流体力学シミュレーションの材料評価への応用
材料の特性を測定する方法のひとつとして、流体がどれだけ通り抜けやすいか、というものがあります。測定には、実際に水や空気、油などの透過性を実験で測定する方法もありますが、X線CT等を用いて取得したデータをもとに、デジタル空間上でシミュレーションする方法も採用可能です。この場合のメリットは、迅速で、実験の再現性が高いこと、条件を仮想的に変化させて繰り返し同じ材料を試験できることなどがあります。一方で、画像の解像度が高まるにつれて計算時間を多く要するようになる点には注意が必要です。
今回は、セグメンテーション後の画像に対して、流体力学シミュレーションを応用した場合に、どのような理論をもとに、どのような洞察が得られるかを紹介していきます。
処理の手順
セグメンテーション画像の準備
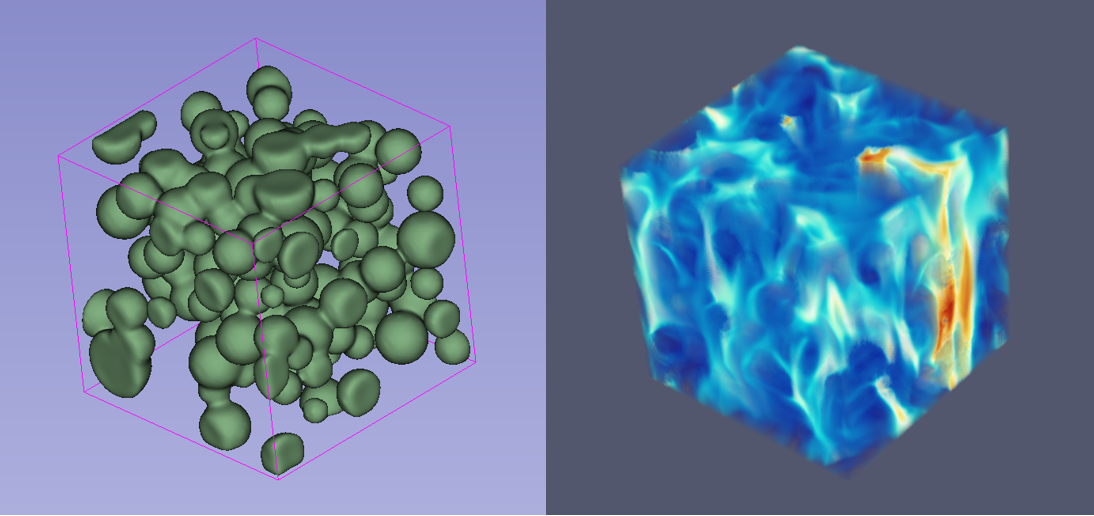
セグメンテーション画像の準備は、シミュレーションの正確性を高めるために重要です。X線CTやMRIなどのイメージング技術を用いて取得した三次元画像データを、材料の固体部分と空隙部分に分ける処理が行われます。この処理により、材料内部の詳細な構造が明らかになり、流体がどのように通過するかをより正確にシミュレートできます。
流体力学シミュレーションの実行
理論
絶対浸透率を数値的に推定するには、ナビエ・ストークス方程式を解きます。粘性率が一定の流れは以下の式で記述できます。
\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{a_f}なお、流体の速度が遅いなど、レイノルズ数が小さい場合には、非線型である対流項
(\mathbf{u} \cdot \nabla) \mathbf{u} が無視できます。この式は、ストークス方程式と呼ばれています。
\frac{\partial \mathbf{u}}{\partial t} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{a_f}非圧縮流体を扱うため、次の制約も課します。
\nabla \cdot \mathbf{u} = 0ここで、
\nablaはナブラ演算子です。勾配を計算する一階の微分作用素です。\nabla^2はラプラシアン演算子です。勾配の発散を計算する二階の微分作用素です。\mathbf{u}は流体相における流体の速度(m/s)です。\nuは流体の動粘性率(m^2/s)です。粘性率(Pa \cdot s)を密度(kg/m^3)で割ったものでもあります。pは物質の流体相における流体の圧力(Pa)です。\rhoは流体の密度(kg/m^3)です。\mathbf{a_f}は外力による加速度(m/s^2)です。
※ 粘性率は、粘度、粘性係数ということがあり、動粘性率は、動粘度、動粘性係数ということがあります。
材料評価における浸透性評価の場合、流体の速度が速い場合は考えず、ストークス方程式を用いることが多いです。したがって、最終的には以下の条件を想定したシミュレーションを実行します。
- 非圧縮性流体: 流体の密度が一定である。
- ニュートン流体: 流体の動粘度が一定である。
- 層流: 流れの速度が低く、乱流を生じない。
境界条件
周期的境界条件を適用することで、固有浸透テンソルの計算が可能になります。また、シミュレーションの過程でフーリエ変換のテクニックが使えるようになり、計算が大きく高速化できるようになります。周期的境界条件を設定する場合、固定の圧力や流量を直接設定せず、流体の全粒子に均等に力を加えることで流れを発生させます。

収束条件
流れの速度が時間の経過とともに変化しなくなるまで、計算をならします。ならしたあとの流れを定常流れと呼びます。流れの速度や圧力の変化が一定の範囲内に収まるまで計算を繰り返します。収束判定には、残差の大きさや収束の速さなどの基準が用いられます。
出力
シミュレーションの出力は、定常流れにおける、流体の速度場や圧力分布のデータが主になります。これらのデータを解析することで、材料の特性を詳細に評価できます。
結果の分析
絶対浸透率(Absolute Permeability)の計算
絶対浸透率は、多孔質材料が単相流体を透過する能力の尺度として定義されます。SI単位は平方メートル(m^2)ですが、平方マイクロメートル (\mu m^2) やダルシー (d) が多く用いられます。1ダルシーは約9.869233×10⁻¹³ m², 9.869233 μm²に相当します。絶対浸透率は、外部条件に依存しない、材料固有の特性です。絶対浸透率k (m^2)は、ダルシーの法則に基づき、流体、流れ、材料パラメータに関連する定数係数として現れます。
k = \frac{Q \mu L}{S \Delta P}Qはボリュームを通過する流量(m^3/s)です。\muは流体の粘性率です(Pa \cdot s)です。Lはサンプルの流れ方向の長さです(m)です。Sはサンプルの断面積です(m^2)です。\Delta Pはサンプル両端の圧力差(Pa)です。
周期境界条件を適用した場合、明示的な圧力差は指定しないので、一定の外力をかけ続けたときに、流量が収束する数値を観察します。粘度が0の場合、または、サンプル中に障害物がない場合、流量が無限になるまで速度が加速してしまい、また、このとき圧力差も生じませんので、絶対浸透率の計算ができないことに注意してください。
計算の準備として、圧力差を計算する方法を先に記述します。ここでは、流体として水を想定します。流体部分に外力による加速度として、重力と同じ9.8 m/s^2が与えられているとき、水の密度1000 kg/m^3を考慮して、高さ1 mあたり、面積1 m^2あたり、98000 kg \cdot m/s^2 = 98000 Nの外力がかかっていることになります。1 Pa = 1 N / m^2ですので、すなわち、高さ1 mにつき、98000 Paの圧力差がある場合に相当することになります。
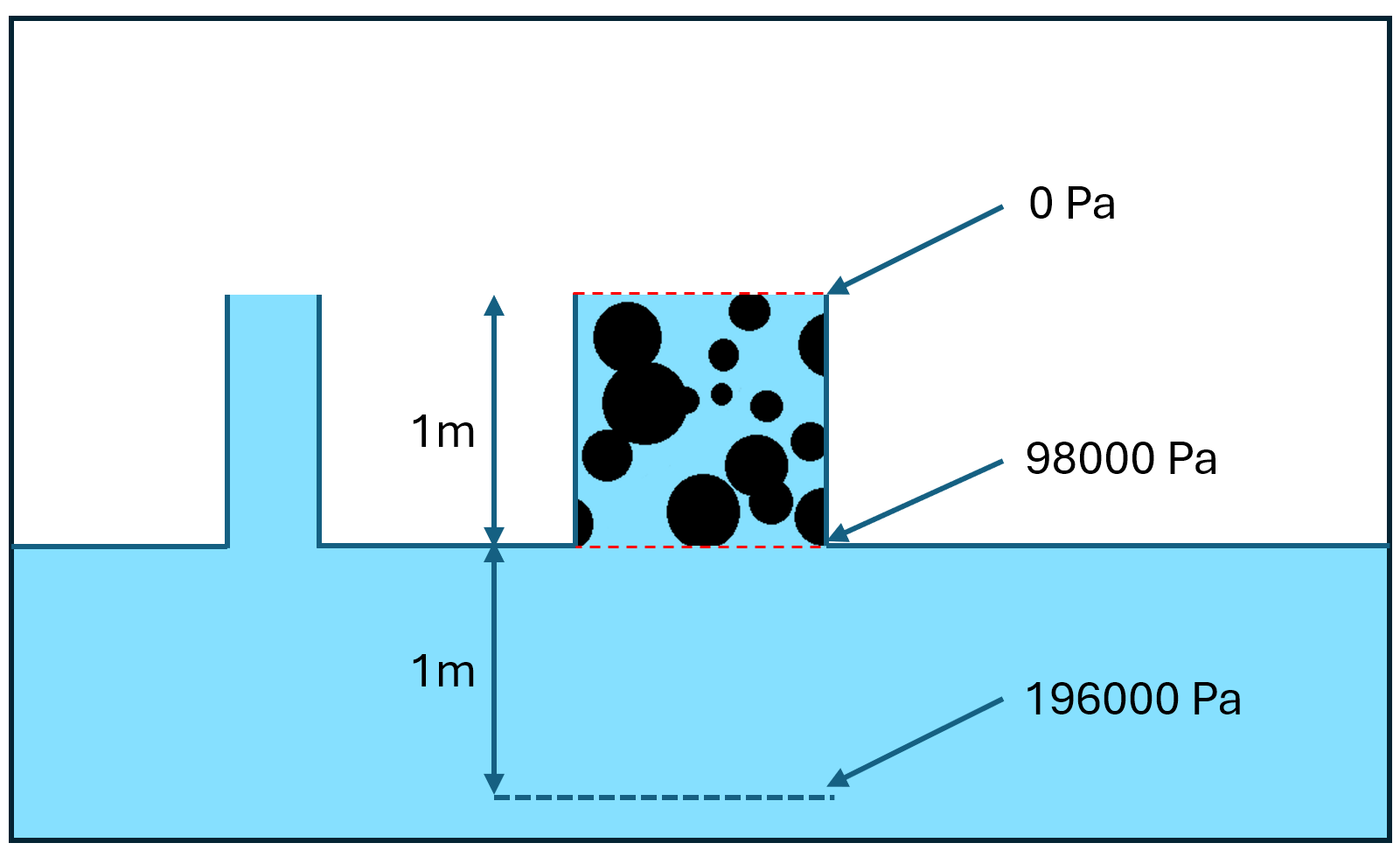
準備ができたところで、典型的な場合の計算例を示します。1辺0.1 mの立方体形状の多孔質サンプルを用いて、流体に水を用い、重力に任せて水を浸透させることを考えます。このケースでは、前段の計算結果から、\Delta P = 9800 Paになります。定常流れに達した状態での流量Q = 50ml/s = 0.00005 m^3/sであったとすると、絶対浸透率k (m^2)は、ダルシーの法則に基づき、次のように計算できます。ここで、水の粘性率は、0.001 Pa \cdot sを用いています。
k = \frac{(0.00005 m^3/s) \times (0.001 Pa \cdot s) \times (0.1 m)}{(0.01 m^2) \times (9800 Pa)} = 5.10 \times 10^{-11} m^2参考までに、絶対浸透率の目安としては、砂利で10^{-7} \sim 10^{-10} m^2、粘土で10^{-11} \sim 10^{-15} m^2程度です。
固有浸透テンソル(Intrinsic Permeability Tensor)の計算
固有浸透テンソルは、空間の任意の方向に沿った浸透率に関する情報となります。これにより、多孔質媒体の異方性が評価できます。
テンソルは、物理量を表現するための数学的な道具であり、スカラー、ベクトル、行列を一般化したものです。浸透テンソルは、3次元空間での多孔質材料の浸透率を記述するために使用され、次のように表されます。
\mathbf{K} = \begin{pmatrix}
k_{xx} & k_{xy} & k_{xz} \\
k_{yx} & k_{yy} & k_{yz} \\
k_{zx} & k_{zy} & k_{zz}
\end{pmatrix}ここで、各要素 k_{ij} は、i方向の圧力勾配がj方向の流れを生成する効果を表します。
固有浸透テンソルを計算するには、3つの直交する方向(x、y、z)での絶対浸透率を計測します。測定には、外力の方向を3パターン用意し、3回シミュレーションを行うことになります。ここで、i≠jの要素k_{ij}を計算する場合、流量Qには、外力の方向とは異なる方向の流量を指定する必要があります。例えば、k_{xy}を計算するには、外力の方向を(x,y,z)=(1,0,0)としたうえで、流量をy平面を通過する流体の量として、計算を行います。
基本的には、計算が正しく行われている場合、この3x3行列は対称性を持ちます。すなわち、k_{ij} = k_{ji}となります。
次に、多孔質媒体の異方性を評価するために、主成分分析(PCA)を使用して固有ベクトルと固有値を計算します。これは、テンソルの対角化を通じて行われ、主成分の方向とそれに対応する浸透率を特定します。
このようにして得られた固有ベクトルは、材料内部の主要な流れの方向を示します。固有値は、各固有ベクトルに対応する浸透率を表します。これらの向きと値は、透過性の観点での材料評価に利用することができます。例えば、3つの固有値が大きくことなる場合、透過性について、異方性が大きいことを示します。
例えば、内部に特定の方向に沿った繊維が分布していたり、特定の方向にそろった平板構造が分布していたりすると、異方性が高く計算されることが多くなります。
曲路率(Tortuosity)の計算
曲路率は、流体が材料内部を通過する際の経路の複雑さを示す指標です。曲路率は、材料の多孔質構造が流体の流れをどれくらい妨げるかを定量的に評価するために用いられます。曲路率の計算には、材料内部の流路の実際の長さと直線距離の比を使用することが直感的ではありますが、すべての流体充填部分の速度ベクトルを取り出し、その大きさの和と、関心のある軸方向のベクトル\mathbf{x}へ射影したときの長さの和との比を計算することで得ることもできます。
tortuosity = \frac{\sum |\mathbf{u}|}{\sum \mathbf{u} \cdot \mathbf{x} }典型的な流路の可視化
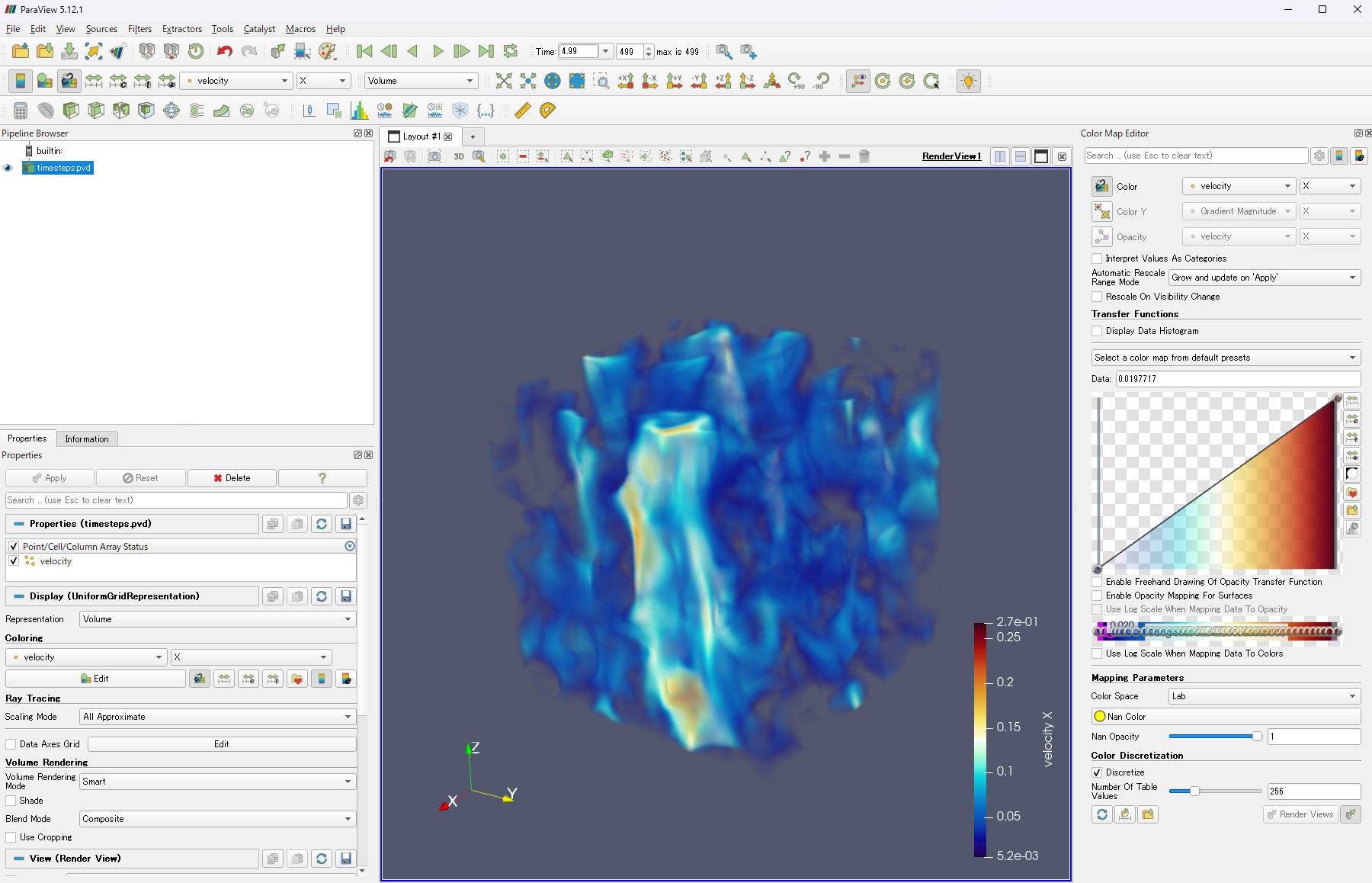
シミュレーションの結果として得られる流体の典型的な流路を可視化することで、材料内部での流れの挙動を直感的に理解できます。これにより、材料の特性や欠陥、改良点などを視覚的に確認することができます。計算結果は、計算に用いたソフトウェア、または、ParaViewなどの専用のオープンソースソフトウェアが適しています。
まとめ
流体力学シミュレーションの出力からは、透過性指標の計算と、異方性の検出ができることを示しました。流体力学シミュレーションは、環境工学や医療分野を含む、幅広い材料科学分野での応用が期待されます。特に、微細構造の解析や新材料の開発において、シミュレーション技術は迅速かつ再現性のある評価を行う上で不可欠なツールとなるでしょう。